Değerli Okurlarım Merhabalar,

Hatırlayacağınız gibi bir önceki makalemizde, Oyun Programcılığına girmek adına çarpışma tekniklerini incelemeye başlamış ve dörtgenlerin çarpışmalarını ele almıştık. Bugünkü makalemizde ise, dairesel şekillerin birbirleri ile olan çarpışmalarını incelemeye çalışacağız. Dairesel şekillerin çarpışmasına verilebilecek en güzel örnek, kaynaklardan edindiğim bilgiye göre Bilardo oyunlarıdır. Burada gerçekten de mükemmel dairelerin birbirleriyle olan çarpışmaları söz konusudur. Şunuda hatırlatmakta fayda var. Şu an için teorilerimizi iki boyutlu uzayda inceliyoruz. Elbetteki işin için üç boyutlu cisimler girdiğinde kullanacağımız algoritmalar ve teknikler birazda olsa farklılık gösterecektir. Çünkü uzay boyutunda X ve Y koordinatlarına ek olarak Z koordinatlarıda işin içine girecektir. Bu da iki boyutlu bir sistemde Bilardo oyunun tasarlanmasının 3 boyutlu sistemdekine göre daha kolay olduğunu göstermektedir.

Dairesel nesnelerin çarpışmalarını belirlemek için eski dostumuz Pisagor Teoreminden faydalanacağız. Burada ana fikir, dairelerin merkezlerinin birbirlerine olan doğrusal uzaklıkları ile yarıçaplarının toplamlarının karşılaştırılmasıdır. Eğer, dairelerin merkezleri arası doğrusal uzaklık, dairelerin yarıçapları toplamından küçük ise, dairelerin üst üste geldiklerinden dolayısıyla çarpıştıklarından söz edebiliriz. Olayı aşağıdaki şekil ile ele almaya çalışalım.

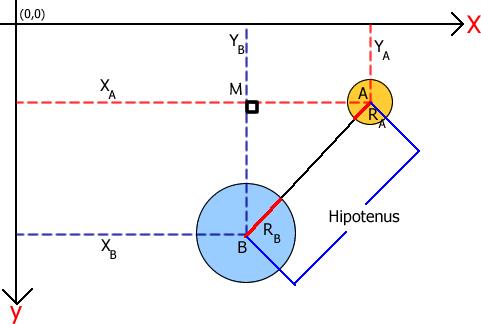
Şekil 1. Dairelerin Çarpışması.

Burada bizim için anahtar şekil, dairelerin merkezleri arasında oluşan BMA dik üçgenidir. Biz bu üçgen yardımıyla, A ve B noktaları arasındaki mesafeyi, başka bir deyişle BMA üçgeninin hipotenüsünü bulabiliriz. Bu bizim için en kilit noktadır. Sonrasında ise, bu mesafeyi Ra ve Rb yarıçaplarının toplamı ile karşılaştırmamız yeterli olacaktır. Dolayısıyla çarpışma formülümüz aşağıdaki gibi olmalıdır.

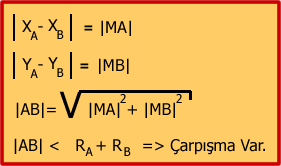
Şekil 2. Çarpışma Teorimiz.

Görüldüğü gibi yapmamız gereken, X ve Y koordinatları arasındaki mesafelerden yararlanarak, üçgenin hiptoneüsünü (yani iki daire merkezi arasındaki doğrusal uzaklığı) bulmak ve bulduğumuz değeri, yarıçapların toplamı ile karşılaştırmaktır. Şimdi dilerseniz, bu teoriyi C# ile geliştirilmiş bir windows uygulamasında nasıl simule edeceğimize bakalım. Geliştireceğimiz uygulama her zamanki gibi basit ve anlamsız olacak. Ancak amacımız, yukarıdaki teoremi uygulamak ve sonuçlarını görmek. Bu amaçla aşağıdaki ekran görüntüsüne ait bir windows uygulaması geliştirdim.

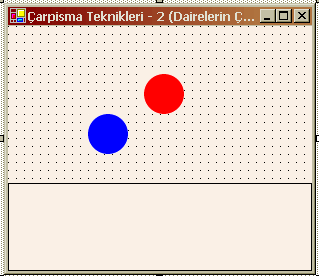
Şekil 3. Uygulama tasarımımız.

Kodlarımız ise aşağıdaki gibi olacaktır.

/*global değişkenlerimizi tanımlıyoruz. */
float Top1_X,Top1_Y,Top2_X,Top2_Y,Top1_R,Top2_R;
double Hipotenus,YaricapToplam;

/*X,Y Koordinatlari ile yariçaplar belirleniyor.*/
private void Hesapla()
{
    Top1_R=Top1.Width/2;
    Top1_X=Top1.Left+Top1_R;
    Top1_Y=Top1.Top+Top1_R;

    Top2_R=Top2.Width/2;
    Top2_X=Top2.Left+Top2_R;
    Top2_Y=Top2.Top+Top2_R;

    float Fark_X=Math.Abs(Top1_X-Top2_X);
    float Fark_Y=Math.Abs(Top1_Y-Top2_Y);

    Hipotenus=Math.Sqrt((Fark_X*Fark_X)+(Fark_Y*Fark_Y));

    YaricapToplam=Top1_R+Top2_R;
}

/* Ölçümleri ekrana yazdırmak için string değer döndüren bir metod hazırlıyoruz.*/
private string Olcumler()
{
    string olcum="Top 1 için X:"+Top1_X.ToString();
    olcum+=" Y:"+Top1_Y.ToString();
    olcum+=" R:"+Top1_R.ToString();
    olcum+=" | Top 2 için X:"+Top2_X.ToString();
    olcum+=" Y:"+Top2_Y.ToString();
    olcum+=" R:"+Top2_R.ToString();
    olcum+=" | Hipotenüs:"+Hipotenus.ToString();
    return olcum;
}

private void frmCollision2_Load(object sender, System.EventArgs e)
{ 
    Hesapla();
    lblOlcumler.Text=Olcumler();
}

/* Form üzerinde A,S,D,W tuşlarına basıldığında, Top2 isimli pictureBox' ın hareket etmesini sağlıyoruz.*/
private void frmCollision2_KeyPress(object sender, System.Windows.Forms.KeyPressEventArgs e)
{
    if(e.KeyChar==(Char)Keys.A)
    {
        Top2.Left-=1;
        Hesapla();
        lblOlcumler.Text=Olcumler();
    }
    if(e.KeyChar==(Char)Keys.D)
    {
        Top2.Left+=1;
        Hesapla();
        lblOlcumler.Text=Olcumler();
    } 
    if(e.KeyChar==(Char)Keys.S)
    {
        Top2.Top+=1;
        Hesapla();
        lblOlcumler.Text=Olcumler();
    }
    if(e.KeyChar==(Char)Keys.W)
    {
        Top2.Top-=1;
        Hesapla();
        lblOlcumler.Text=Olcumler();
    }
    Kontrol();
}

/* Çarpışma kontrolümüzü yapıyoruz. */
private void Kontrol()
{
    if(Hipotenus<YaricapToplam)
    {
        this.Text="";
        this.Text+=" |!!! ÇARPISMA VAR !!!| ";
    }
    else
        this.Text="";
}

Kodlarımız son derece açık. Dikkat etmemiz gereken noktalardan birisi, Top1 ve Top2 isimli nesnelerin X ve Y koordinatlarının bulunmasıdır. Burada Left ve Top özelliklerinin yanısıra daire merkezlerini tam olarak bulabilmek için, Width veya Height (daire olduklarından X veya Y' ye eklenecek mesafelerin Width veya Height ile hesaplanması farketmez) değerlerinden birisinide göz önüne almamız gerekir. Yani aşağıdaki kodlarda olduğu gibi;

Top1_R=Top1.Width/2;
Top1_X=Top1.Left+Top1_R;
Top1_Y=Top1.Top+Top1_R;

Top2_R=Top2.Width/2;
Top2_X=Top2.Left+Top2_R;
Top2_Y=Top2.Top+Top2_R;

Bunun dışında Hipotenüs hesaplamasında elbetteki karekök almak için Math sınıfının Sqrt fonksiyonundan yaralanmaktayız.

Hipotenus=Math.Sqrt((Fark_X*Fark_X)+(Fark_Y*Fark_Y));

Uygulamamızı çalıştırdığımızda, Top2 isimli nesneyi herhangibir yönden Top1 isimli nesne üstüne getirirsek çarpışmanın meydana geldiğini kolayca tespit edebiliriz.

Şekil 4. Çarpışmanın çalışma zamanında tespit edilmesi.

Çarpışmalar ile ilgili bir diğer önemli durumda, dörtgenler ile dairelerin çarpışmalarının nasıl tespit edilebileceğidir. Bu kez, daire merkez nesne olarak düşünülür ve dörtgenin daireye olan en yakın ve en uzak noktaları değerlendirilerek çarpışmanın olup olmadığına bakılır. Bu teoriyide bir sonraki makalemizde incelemeye çalışacağız. Tekrardan görüşünceye dek hepinize mutlu günler dilerim.