Değerli Okurlarım Merhabalar,

Yaklaşık bir ay kadar önce evde dinlenirken, şu ana kadar yaptığım işleri ve projeleri düşündüm. Kesin olarak şunu söyliyebilirim ki, profesyonel anlamda ilgilendiğim ve kullandığım tek dil C# idi. C# dilini kullanarak, .Net platformu altında veritabanı ağırılıklı olmak üzere çeşitli çalışmalar yaptım. Ancak bir süre sonra farkettim ki, bir Matematik Mühendisi olarak lisans eğitimim sırasında gördüğüm o devasa cebir problemleri, teorem ispatları hiç bir zaman işin içine girmemişti. Matematiğin belkide çok az olmakla birlikte dört işleminin ve bir takım algoritmalar için gerekli iteratif ifadelerinin yer aldığı uygulamalar dışında, onu çok yoğun şekilde kullanmamıştım.

Belki finansal veya istatistiki bir projede yoğun olarak ekonomi teoremlerini ve bunlara bağlı olarak matematiksel denklemleri kullanmak gerekmekteydi ancak çok yoğun bir şekilde bunları kurcalamamıştım. Düşündükçe, günümüz dünyasında artık algoritmalar ile, matematik ile uğraşan yazılımcıların azaldığı kanısına vardım. Hepimizde matematik temeli var. Hepimiz bu konuda çeşitli sınavlardan geçtik. Ama sonuç itibariyle çok az projede, daha önceden gördüğümüz eşsiz teoremleri kullandık. O dakikalarda neden bu yöne eğilmiyorum, biraz eğlenceli hatta matematik yüklü çalışmalara el atmıyorum diye düşünmeye başladım. Derken çözümü son derece eğlenceli ama bir o kadarda önemli bir sahada buldum. Oyun Programcılığı.

Çoğumuz, yazılım geliştirirken bir gün büyük bir oyunu yazan ekibin içinde olmayı, onun geliştiricilerinden birisi olarak anılmayı hayal etmişizdir. Bu çok çalışmayı ve birazda zeki olmayı gerektiren bir kişilik ister. Kendi kendime düşünürken, elbette günümüzün popüler oyunlarından birisini yazan herhangibir ekipte olabilmek için çok erken olduğunu zaten biliyordum. Ama en azından bir oyun için gerekli en temel bileşene biraz da olsa aşinalığım vardı. Matematik. Oyun programlama içerisinde, oyun motorlarının geliştirilmesinden aksiyonların uygulanışına, yapay zeka taktiklerinden stratejik karar mekanizmalarına kadar her aşamada Matematiksel algoritmaların yer aldığını gayet iyi biliyordum. Benim için bunları öğrenmeye çalışmak, uygulamak ve denemek, benim için heyecan verici olacaktı. Diğer taraftan eski Matematik günlerimi hatırlamış bir başka deyişle saksıyı biraz daha çalıştırmış olacaktım.

Büyük bir hevesle bir taslak plan hazırladım ve işe koyuldum. Bana öncelikle oyun programlamadaki temel teknikleri başlangıç seviyesinden itibaren anlatacak ve yeri geldiğinde de uzmanlık seviyesine kadar çıkartacak kitaplar gerekliydi. Hemen Amazon.com' da kısa bir araştırmadan sonra aşağıdaki kitapların siparişlerini verdim.

Oyun Programlama İle İlgili Kaynak Kitaplar
	Beginning .Net Game Programming in C# APress David Weller, Alexandre Santos Lobao, Elen Hatton 414 Sayfa Amazon Fiyatı : 30.59$
	C# and Game Programming: A Beginner's Guide AK Peters Ltd. Salvatore A. Buono 592 Sayfa Amazon Fiyatı : 39$
	Beginning C# Game Programming (Game Development) Muska & Lipman/Premier-Trade Ron Penten 344 Sayfa Amazon Fiyatı : 20.39$
	Managed DirectX 9 Kick Start : Graphics and Game Programming Sams Tom Miller 432 Sayfa Amazon Fiyatı : 23.79 $

Bu anlattığım olaylar yaklaşık bir ay kadar önce gerçekleşti. Şu anda bu kitaplarda az da olsa ilerlemiş durumdayım. İnanın sevgili okurlarım bu işe giriştiğim için çok ama çok memnunum. Biraz matematik, biraz teori biraz pratik derken bir şeyler kapmaya başladım bile. Herşeyden önce ilk konularda, eski dostumuz Hipotenüs' ü görmek bile son derece güzeldi. Konuları anlamaya başladığıma göre şimdi tek yapmam gereken öğrendiklerimi uygulayarak pekiştirmek ve sizler ile paylaşmak. Artık bu kadar laf kalabalığından sonra, bu makalemizin konusunada değinme zamanı geldi.

Bu gün, oyun programlamanın önemli temellerden birisi olan Çarpışma (Collision) tekniklerine giriş yapacağız. Bir oyunda, bir birinden bağımsız öğelerin bir birleriyle çarpışmaları üzerinde duracağımız asıl konu olacak. Bir savaş oyununda tarafların bir birlerine karşı yaptıkları hamleler sonucu kimin kime vurduğunu tespit etmek, vuruşların yönüne veya şiddetine göre, darbeyi alan nesnelerin ne tür hareketlerde bulunacağına karar vermek açısıdından Çarpışma teknikleri gerçekten önemlidir. Bu teknikler bir kaç tanedir. Bu gün ben sizlere, 2  boyutlu koordinat sisteminde dörtgensel şekillerin çarpışmalarının nasıl tespit edilebileceğini anlatmaya çalışacağım.

Dortgenlerin baz alındığı bu teknikte amaç, objeleri içine alan ve sınırlayan dörtgensel alanların birbirleri üstüne gelip gelmediklerinin tespit edilebilmesidir.

Öncelikle durumu analiz edebilmek amacıyla aşağıdaki şekli göz önüne alalım.

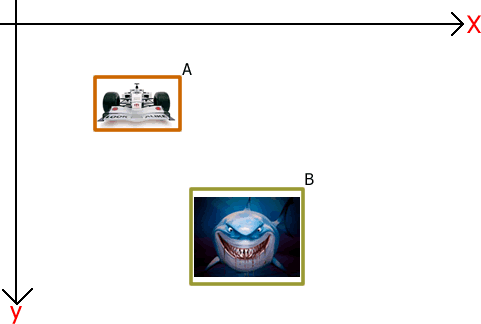
Şekil 1. Senaryo.

Senaryo gereği, köpek balığı ve yarış arabası nesnelerimizin hareketli olduklarını düşünelim. Burada, yarış arabası ve köpek balığı aslında ekranda piksel olarak yer kaplamaktadır. Bu iki piksel topluluğunun çarpışıp çarpışmadıklarını test edebilmek için kullanılabilecek en basit teknik, nesnelerin çevresini saran dörtgenlerin bir birleri üstüne gelip gelmediklerini tespit etmektir. Bu nedenle, senaryomuzda yarış arabımızı A isimli, köpek balığımızı ise B isimli dörtgenler ile çevrelediğimizi düşünelim. İşte bu noktadan sonra işin içine biraz matematik girecek.

Eğer bu iki nesnenin X koordinatları arasındaki fark, genişliklerinin yarılarının toplamından küçük ise ve iki nesnenin Y koordinatları arasındaki fark, yüksekliklerinin yarılarının toplamından küçük ise, bu iki dörtgen üst üste gelmiş dolayısıyla çarpışma (Collision) gerçekleşmiş demektir.

Bunun matematiksel olarak aşağıdaki şekil ile daha iyi anlayabiliriz.

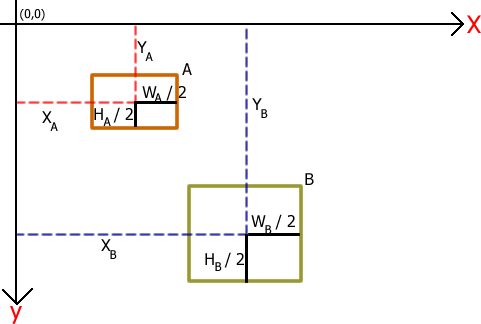
Şekil 2. Koordinat, genişlik ve yükseklik ölçüleri.

Burada, her iki dörtgenin ekranın sol üst köşesine olan uzaklıkları ve genişlik ile yükseklikleri belirtilmektedir. Elbette bir nesnenin X koordinatı uygulamada bu nesnenin Left özelliğinin değerine, Y koordinatı ise Top özelliğinin değerine işaret etmektedir. Aynı şekilde genişlik için Width, yükseklik için ise Height özelliklerinden yararlanılacaktır. Yukarıda bahsettiğimiz çarpışma koşulunun matematiksel ifadesi ise aşağıdaki gibi olacaktır.

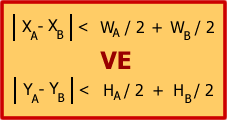
Şekil 3. Çarpışma (Collision) koşulları.

Dikkat edecek olursanız eşitsizliklerin sol taraflarındaki ifadelerde mutlak değer söz konusudur. Bu nedenle Math sınıfının Abs isimli metodu işimize çok yarayacaktır. Bu ifadedeki her iki eşitsizliğinde gerçekleşmesi halinde, dörtgenlerin üst üste geldiklerinden, dolayısıyla çarpıştıklarından söz edebiliriz. Bu teorimin gerçekliğini kontrol etmenin en güzel yolu uygulama üzerinde olacaktır. Bu amaçla aşağıdaki gibi basit bir windows uygulaması oluşturdum.

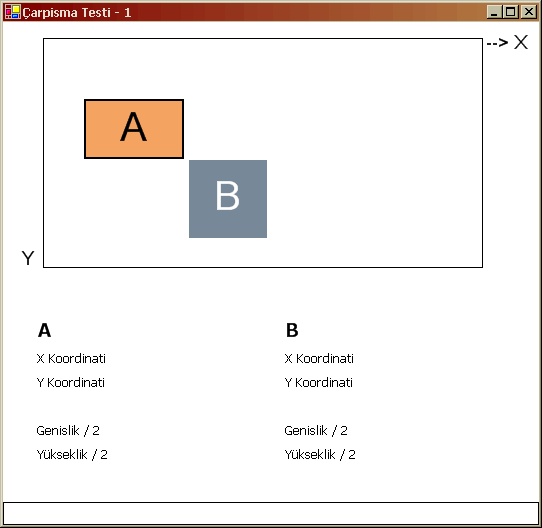
Şekil 4. Uygulama.

Bu uygulamada, A isimli dörtgen nesnesini klavyedeki A,S,D,E tuşları ile hareket ettirebileceğiz. Bizim buradaki amacımız, Çarpışma olduğu takdirde bunun gerçekleşip gerçekleşmediğini tespit edebilmek. Bu amaçla, nesnelerin ekrandaki koordinatlarınıda izlediğimiz label nesnelerimiz var. Gelelim uygulamamızın kodlarına.

private void Yaz()
{
    lblXA.Text=A.Left.ToString();
    lblYA.Text=A.Top.ToString();
    lblWidthA.Text=Convert.ToString((A.Width/2));
    lblHeightA.Text=Convert.ToString((A.Height/2));

    lblXB.Text=B.Left.ToString();
    lblYB.Text=B.Top.ToString();
    lblWidthB.Text=Convert.ToString((B.Width/2));
    lblHeightB.Text=Convert.ToString((B.Height/2));
}

private void frmCarpisma_Load(object sender, System.EventArgs e)
{
    Yaz();
}

/* Çarpışma Kontrolünün gerçekleştirildiği metod */
private bool CarpismaKontrol()
{
    float mutlakX=Math.Abs((A.Left+(A.Width/2))-(B.Left+(B.Width/2)));
    float mutlakY=Math.Abs((A.Top+(A.Height/2))-(B.Top+(B.Height/2)));

    float farkGenislik=(A.Width/2)+(B.Width/2);
    float farkYukselik=(A.Height/2)+(B.Height/2);

    if((farkGenislik>mutlakX)&&(farkYukselik>mutlakY))
    {
        return true;
    }
    else
        return false;
    } 
}
private void frmCarpisma_KeyPress(object sender, System.Windows.Forms.KeyPressEventArgs e)
{
    if(e.KeyChar==(Char)Keys.D)
    {
        A.Left+=10;
    }
    if(e.KeyChar==(Char)Keys.A)
    {
        A.Left-=10;
    }
    if(e.KeyChar==(Char)Keys.W)
    {
        A.Top-=10;
    }
    if(e.KeyChar==(Char)Keys.S)
    {
        A.Top+=10;
    }
    
    Yaz();
    if(CarpismaKontrol())
    {
        lblCarpismaKontrol.Text="Çarpisma var...";
    }
    else
    {
        lblCarpismaKontrol.Text="";
    } 
}

Uygulamada dikkat ederseniz, teoremi aşağıdaki kod satırlarındaki gibi uyguladık.

float mutlakX=Math.Abs((A.Left+(A.Width/2))-(B.Left+(B.Width/2)));/* X koordinatları arası farkın mutlak değeri. */
float mutlakY=Math.Abs((A.Top+(A.Height/2))-(B.Top+(B.Height/2)));/* Y koordinatları arası farkın mutlak değeri . */

float farkGenislik=(A.Width/2)+(B.Width/2); /*Genişliklerin yarılarının toplamı.*/
float farkYukselik=(A.Height/2)+(B.Height/2); /* Yüksekliklerin yarılarının toplamı. */

if((farkGenislik>mutlakX)&&(farkYukselik>mutlakY)) /* Eğer koşul doğru ise çarpışma vardır. */
{
   return true;
}
else
   return false;
}

Şimdi uygulamamızı test edelim. A, S, D, W tuşları ile (bunlara basarken Caps Lock açık olmalı) A isimli buton kontrolümüzü 10' ar birim hareket ettirebilmekteyiz. Eğer kutuları üstüste getirirsek çarpışma teoreminin başarılı bir şekilde gerçekleştiğini görürüz.

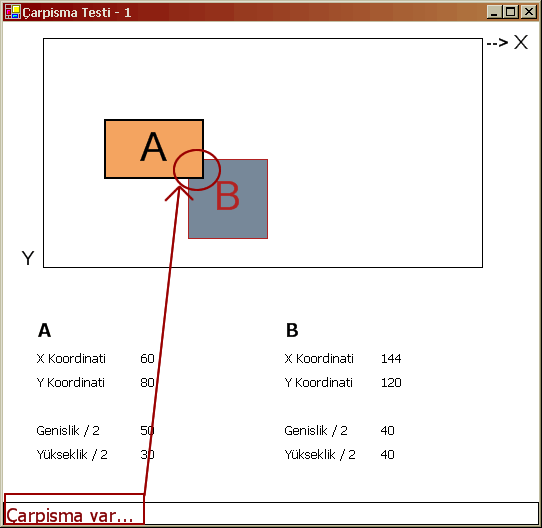
Şekil 5. Çarpışma gerçekleşti.

Bu teknik en basit çarpışma modelidir. Nesnelerin dörtgenler içerisinde düşünülmesi araba şeklinde olduğu gibi, boşluğa denk düşen alanlarında hesaba katılmasına neden olmaktadır. Ancak iş dairesel nesnelerin çarpışmasına geldiğinde (örneğin tenis toplarının raketler çarpması) hatta, daire ve karesel nesnelerin çarpışmasına geldiğinde dahada karmaşıklaşmaktadır.

Artık ilerleyen zamanlarda bu teoremleri incelemeye çalışacağım. Öğrendikçede siz değerli okurlarıma aktaracağım. Artık 24 bölümmü sürer bir tetris oyunu yazmamız, 24 ay mı sürer bilemiyorum. En azından daha önceden bildiğim hatta mutlaka bildiğim ama farkına varamadığım algoritmaları öğrenmek beni oldukça memnun etti. Umuyorum ki sizlerde bu yazı dizisinden hoşnut kalırsınız. Tekrar görüşünceye dek hepinize mutlu günler dilerim.