Değerli Okurlarım Merhabalar,
Geçtiğimiz hafta boyunca, Oyun Programcılığı ile ilgili olaraktan aldığım kitapları fırsat buldukça okumaya ve çalışmaya devam ettim. Konular o kadar heyecanlı ve sürükleyici ki araştırmak için zaman kavramı anlmasız hale geliyor. Öyleki, dün gece sabaha karşı saat 03:00 sularında kağıt kalem ile boğuşuyor ve Çarpışma Tekniklerinden birisinin daha matematiksel modelinin C# ile nasıl uygulanabileceğini araştırıyordum. Sonuç olarak işe bir kaç saatlik uykuyla gitmek zorunda kaldım. Ancak buna rağmen tüm gün dinçtim. Çünkü, çarpışma tekniklerinden birisini daha öğrenmiştim. Sıra anlatmaya gelmişti. İşte bugünkü makalemizde 3ncü çarpışma tekniğini incelemeye çalışacağız.
Oyun programcılığında önemli bir yere sahip olan çarpışma tekniklerinde, bu makaleye gelinceye kadar iki ana konuyu inceleme fırsatı bulduk. İlk olarak iki dörtgensel nesnenin bir birleriyle olan çarpışmalarını inceledik. Daha sonraki makalemizde ise, eski dostumuz Pisagor' u anıp, iki dairesel nesnenin birbirleriyle olan çarpışmalarını araştırdık. Sırada bu iki durumun kombinasyonu var. Yani, bir dörtgen ile dairesel bir nesnenin birbirleriyle olan çarpışmalarının tespit edilmesi. Bu teknikte yine Pisagor teroeminden yararlanacağız. Ancak dikkat etmemiz gereken önemli koordinat noktaları var. Bu durumu daha iyi analiz etmek için aşağıdaki şekli göz önüne alalım.
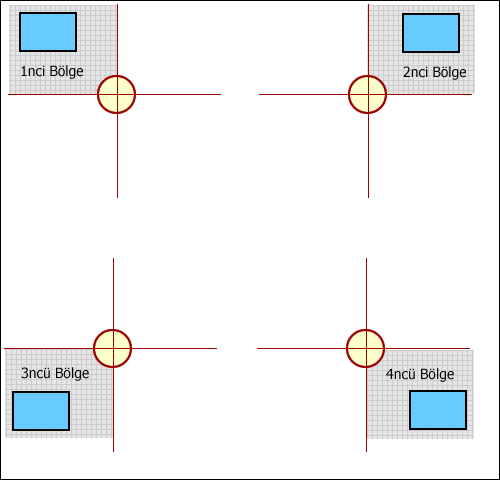
Şekil 1. Dört Bölge.
Bu teoride, dörtgenin dairesel nesneye göre olan konumlarını ele almamız gerekiyor. Bu da bizim, dörtgen nesnesine ait olan maksimum ve minimum sınır noktalarını bilmemiz gerektiğini göstermektedir. Buna göre, dörtgensel nesnenin köşe noktalarının x ve y koordinatları ele alınır. Kısaca, oluşturacağımız pisagor üçgeni için bu maksimum ve minimum x, y koordinatlarını bilmemiz gerekiyor. Çarpışma teoremine gelince;
 |
Dörtgenin dairesel nesneye en yakın olan köşe noktalarından yola çıkılarak oluşturulan dik üçgene ait hipotenüs değeri, dairesel nesnenin yarıçapından küçük ise çarpışma vardır. |
Şimdi buradaki dört bölgeyi kısaca inceleyelim. Örnek olarak 4üncü bölgeyi aşağıdaki şekilde olduğu gibi ele alabiliriz. Esasen tüm bölgelerde, dörtgensel nesneye ait minX,maxX,minY ve maxY koordinatları büyük öneme sahiptir. Örneğin PRO üçgenini göz önüne aldığımızda, kenarların uzunluklarını bulabilmek için R noktasının koordinatlarından yararlanılmaktadır. R noktasına dikkat edecek olursanız, dörtgenin en uzak X ve en uzak Y değerlerine sahip olduğunu görürsünüz. Dolayısıyla biz, PO uzaklığını bulmak istiyorsak, Ox değerinden RmaxX değerini çıkartmamız gerekecektir. Aynı durum RP kenarının boyunu bulurken de geçerlidir. Bu durumda, Oy değerinden RmaxY değerini çıkartırız. Burada dörtgenin dördüncü bölgeye düştüğünü anlamak için dairenin x,y koordinatları ile R noktasının koordinatları karşılaştırılır. Burada dikkat etmemiz gereken husus, R noktasının koordiantlarını dörtenin daireye olan konumuna göre değişeceğidir.
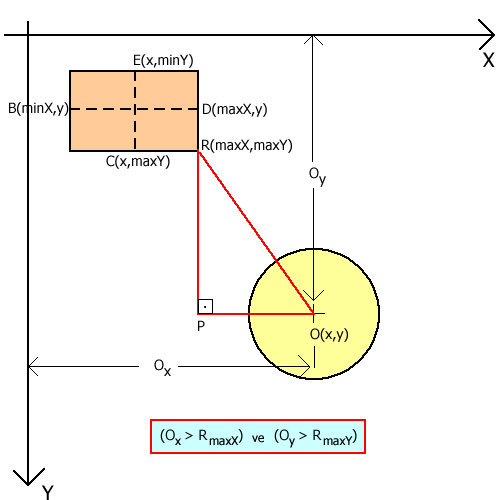
Şekil 2. Dördüncü bölge için durum.
Bu anlattıklarım size biraz karmaşık geldiyse sıkı durun. Diğer bölgelerin grafiksel ifadeleride aşağıda yer almaktadır. Dikkat edecek olursanız, R noktasının koordinatları her bölge için farklıdır. Buda üçgene ait dik kenarlar hesaplanırken uygun R noktası koordinatlarını kullanmamız gerektiğini, başka bir deyişle programlama algoritmasınıda, söz konusu bölgeleri if koşulları ile tespit ederek geliştirmemiz gerektiğini gösterir.
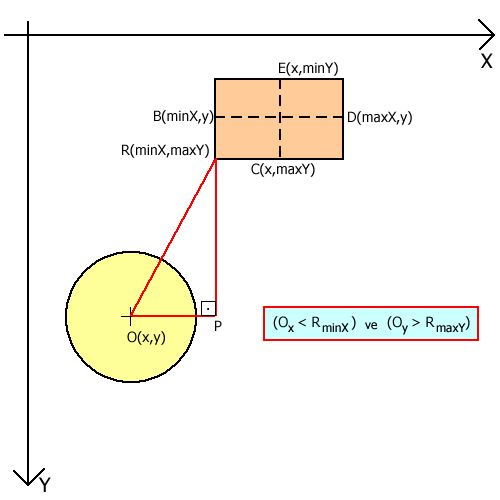
Şekil 3. Üçüncü bölge için durum.
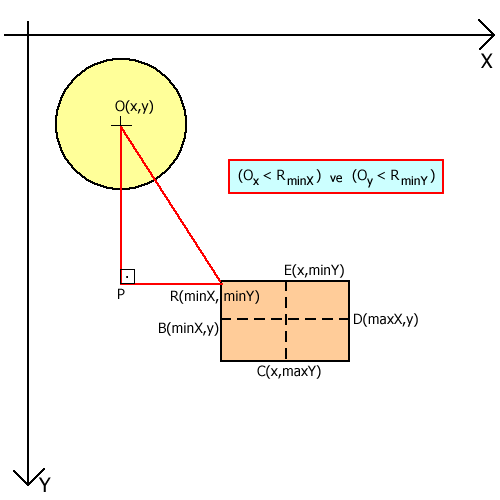
Şekil 4. Birinci bölge için durum.
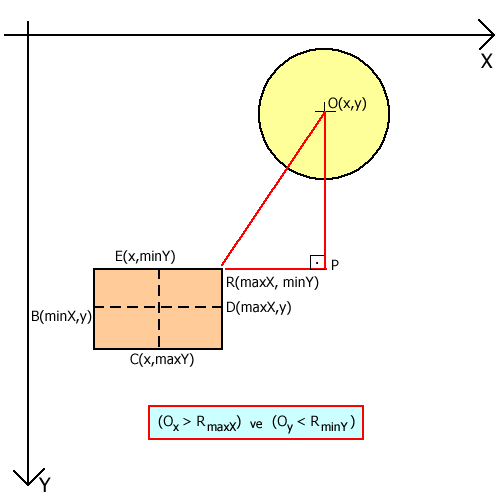
Şekil 5. İkinci bölge için durum.
Şimdi sıra geldi bu teoremi C# kodları ile gerçekleştirmeye. Bu amaçla aşağıdaki ekran görüntüsüne sahip basit bir windows uygulaması geliştirdim. Her zamanki gibi işlemleri kolaylaştırmak amacıyla, dairesel nesneyi sabit tutup, dörtgensel nesneyi A,S,D,W tuşları ile hareket ettiriyorum. Bizim için önemli olan kısımlar, 4 durumdada geçerli olan üçgene ait dik kenarların FarkX ve FarkY şeklinde hesap edilmeleri ve buradan yola çıkılarak hipotenüs değerlerinin bulunması. Son olarak bu hipotenüs değerini, dairenin yarıçapı ile karşılaştırıp çarpışma olup olmadığını inceliyoruz.
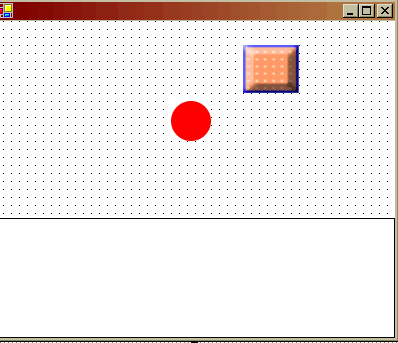
Şekil 6. Uygulama formu.
Şimdi gelelim uygulama kodlarımıza.
/*global degiskenlerimizi tanimliyoruz. */
float Daire_X,Daire_Y,Dortgen_X,Dortgen_Y,Daire_R;
float Dortgen_MinX,Dortgen_MaxX,Dortgen_MinY,Dortgen_MaxY;
double Hipotenus,FarkX,FarkY;
/*Daire için X,Y koordinatlar, yarıçap Dörtgen için ise X,Y, minimum ve maksimum X,Y koordinatları hesaplanıyor.*/
private void Hesapla()
{
Daire_R=Daire.Width/2;
Daire_X=Daire.Left+Daire_R;
Daire_Y=Daire.Top+Daire_R;
Dortgen_X=Dortgen.Left+Dortgen.Width/2;
Dortgen_Y=Dortgen.Top+Dortgen.Height/2;
Dortgen_MinX=Dortgen.Left;
Dortgen_MaxX=Dortgen.Left+Dortgen.Width;
Dortgen_MinY=Dortgen.Top;
Dortgen_MaxY=Dortgen.Top+Dortgen.Height;
/*Burada temel olarak, dörtgenin hangi bölgelere denk düştüğüne bakarak dik üçgene ait FarkX ve FarkY değerlerini hesap ediyoruz.*/
if(Daire_Y<Dortgen_MinY)
{
FarkY=Daire_Y-Dortgen_MinY;
}
if(Daire_Y>Dortgen_MaxY)
{
FarkY=Daire_Y-Dortgen_MaxY;
}
if(Daire_X>Dortgen_MaxX)
{
FarkX=Daire_X-Dortgen_MaxX;
}
if(Daire_X<Dortgen_MinX)
{
FarkX=Daire_X-Dortgen_MinX;
}
/*Dik üçgene ait hipotenüsü buluyoruz.*/
Hipotenus=Math.Sqrt((FarkX*FarkX)+(FarkY*FarkY));
}
/* Ölçümleri ekrana yazdirmak için string deger döndüren bir metod hazirliyoruz.*/
private string Olcumler()
{
string olcum="Daire için X:"+Daire_X.ToString();
olcum+=" Y:"+Daire_Y.ToString();
olcum+=" R:"+Daire_R.ToString();
olcum+=" | Dortgen İçin X:"+Dortgen_X.ToString();
olcum+=" Y:"+Dortgen_Y.ToString();
olcum+=" | Dortgen İçin MinX:"+Dortgen_MinX;
olcum+=" | Dortgen İçin MaxX:"+Dortgen_MaxX;
olcum+=" | Dortgen İçin MinY:"+Dortgen_MinY;
olcum+=" | Dortgen İçin MaxY:"+Dortgen_MaxY;
olcum+=" | Hipotenüs:"+Hipotenus.ToString();
return olcum;
}
/* Form üzerinde A,S,D,W tuslarina basildiginda, Dortgen isimli pictureBox' in hareket etmesini sagliyoruz.*/
private void frmCollision2_KeyPress(object sender, System.Windows.Forms.KeyPressEventArgs e)
{
if(e.KeyChar==(Char)Keys.A)
{
Dortgen.Left-=1;
Hesapla();
lblOlcumler.Text=Olcumler();
}
if(e.KeyChar==(Char)Keys.D)
{
Dortgen.Left+=1;
Hesapla();
lblOlcumler.Text=Olcumler();
}
if(e.KeyChar==(Char)Keys.S)
{
Dortgen.Top+=1;
Hesapla();
lblOlcumler.Text=Olcumler();
}
if(e.KeyChar==(Char)Keys.W)
{
Dortgen.Top-=1;
Hesapla();
lblOlcumler.Text=Olcumler();
}
Kontrol();
}
/* Çarpisma kontrolümüzü yapiyoruz. */
private void Kontrol()
{
if(Hipotenus<Daire_R)
{
this.Text="";
this.Text+=" |!!! ÇARPISMA VAR !!!| ";
}
else
this.Text="";
}
Kodlarımız son derece açık ve kolay. Uygulamamızı çalıştırdığımızda, çarpışma teorimizin başarılı bir şekilde çalıştığını görürüz.

Şekil 7. Çarpışma durumu.
Görüldüğü gibi artık oyun programlamada önemli noktalardan birisi olan çarpışma teorilerinde bayağı bir yol aldık. Ancak her zaman bu teknikleri kullanmayacağız. Örneğin zaman zaman, ekranın eşit karelere bölündüğünü (aynı kareli defterler gibi) ve nesnelerin bu kareler üzerindeki konumlarına göre çarpışıp çarpışmadıklarının belirlendiğini öğrendim. Önümüzdeki hafta büyük bir ihtimalle bu konuyu incelemeye çalışacağım. Kaynaklardan incelediğim kadarı ile bu karelere bölme tekniği tam anlamıyla PackMan tarzı oyunlara yönelik geliştirilmiş bir model. İşin içine bu kez matris dizileri girecek. Bakalım başımıza neler gelicek. Tekrardan görüşünceye dek hepinize mutlu günler dilerim.