 Merhaba Arkadaşlar,
Merhaba Arkadaşlar,
Satranç oynamayalı yıllar olmuştur. Lise yıllarında kadim dostum Burak Gürkan ile karşılıklı maçlar yapardık. Kerata çok iyiydi. Maçları çoğunlukla kaybederdim ama yine de hoşuma giderdi onunla rekabet içerisine girmek(Bir ara arayayım da yine satranç oynayalım) Herhalde sevdiğimiz bir arkadaşımızla yapabileceğimiz en güzel aktivitelerden birisidir Satranç. Sebat etmek, stratejik düşünmek, saygı göstermek, kabullenmek, odaklanmak…Faydaları saymakla bitmez.
En faal oynadığımız yıllar 1990 ile 1993 arasındaydı. O zamanlar Burak ailesi ile Kadıköy’ün sakin sokaklarından birisinde oturuyordu. Sabahçı olduğumuz için öğleden sonraları zaman zaman evlerine giderdim. Annesi Nimet Hanım’ın lezzetli sütlü kahvesi yanında mutlaka tahinli çörek olurdu. Eğer evdeyse de Ertan amcamızla salonda hoş bir muhabbetin içerisine dalardık. Bize Galatasaray’daki futbolculuk yıllarından, Altay’dan bahsederdi. Burağın odası arka bahçeye doğru bakardı. Herhalde hayatımın orada geçen hiç bir anında tek çıt dahi duymamışımdır. Sakinliği ile huzur veren bir odaydı. O günleri özlediğimi itiraf edebilirim. Çok fazla ve hatta neredeyse hiç problemimiz yoktu(Üniversite sınavı, okul dersleri ve kızlardan başka)
Geçenlerde o günlerin özlemiyle dünya satranç federasyonunun sayfasında gezinirken buldum kendimi. Benim bildiğim en meşhur satranç ustaları Garry Kasparov, Anatoly Karpov, Bobby Fischer ve IBM Deep Blue idi :) Derken şu adreste güncel bir Top 100 listesine rastladım. Magnus birinci, Fabiano ikinci, Mamedyarov üçüncü ve bu şekilde 100ncü sıraya doğru giden bir liste. O anda farkettiğim ve aslında cep telefonlarımızda oynadığımız oyunlardan, basketbol maçlarındaki istatistiklere kadar hep etrafımızda olan bir veri dikkatimi çekti. Rating…Nasıl hesaplanıyordu? Her grup kendi kafasına göre mi hesaplıyordu? Bunun genel kabul görmüş bir algoritması yok muydu? Varsa formülünü kim icat etmişti? Hangi alanlarda kullanılıyordu?
Araştırmalarıma devam ettikçe güzel bulgulara ulaştım. İşin içinde tabiki matematik de vardı. Meğer Birleşik Devletler Satranç Federasyonu’nun kurucusu olan Prof. Arpad Elo’nun kendi adıyla anılan bir eşitliğinden yararlanılıyormuş. Newyork Times'ın haberine göre kendisi 1992 yılının 5 Kasım günü evinde geçirdiği kalp krizi nedeniyle hayatını kaybetmişti. Belki de o gün arka bahçeye bakan odada ebedi dostum ile satranç oynuyorduk.
Hemen denklemin nasıl çalıştığını öğrenmeye başladım. Problem birbirleriyle rekabet halinde olan yarışmacıların, aralarında yaptıklara maçlara göre nasıl puanlanabileceğiyle(derelecendirilebileceğiyle) ilgiliydi. Çözüm için öncelikle birbirlerine karşı yaptıkları bir maçı kazanma ve kaybetme olasılıklarının yüzdesel olarak hesaplanması gerekiyor. Sonrasında bu ELO değerinden yararlanılarak, grubun genellikle 10 ile 32 arasında belirleyeceği bir katsayıya göre ikinci bir eşiltiğin işletilmesi gerekiyor ki puanları güncelleyebilelim.
Konuyu bir örnek üzerinden incelemek en güzeli değil mi? Dünya sıralamasının birinci ve ikinci sırasındaki yarışmacıların aralarında yapacakları maçın sonuçlarını irdelemeye çalışalım. Norveçli satranç ustası Magnus Carlsen’in yazıyı yazdığım tarih itibariyle 2839 puanı vardı. Amerikalı Fabiano Caruana’nın puanı ise 2827. Bu iki kişinin güncel puanlarına göre ELO rating değerlerini aşağıdaki gibi hesaplayabiliriz(Bence kalemi kağıdı çıkartın, sizde benimle birlikte hesaplamaya çalışın. Belki uygularken bir yerlerde hata yapmışımdır)

Magnus’un Fabiano ile yapacağı maçı kazanma olasılığı %52. Fabiano içinse bu oran %48. Çok doğal olarak yüzdesel olarak ifade edilen kazanma olasılıklarının toplamının 1e tamamlanması gerekiyor. Formülde her iki oyuncunun güncel puanlarına başvuruluyor. Bunlar formülün değişken parçaları. Ancak formülün kalan kısmındaki tüm sayılar sabit değerler. Bu hesaplama ile kazanma ihtimallerini çıkartmış ve ilk aşamayı tamamlamış olduk.
Derken maç günü geldi çattı. Sovyet döneminin izlerini taşıdığı her halinden belli olan büyük basketbol sahasının tam orta yerindeki satranç masasında karşılıklı oturan iki kişi vardı. Hemen yanlarında duran hakem ve etrafı çevrelemiş onlarca seyirci heyecanlı bir şekilde karşılaşmanın başlamasını bekliyordu. Kameraman önce satranç tahtasındaki bir piyona odaklandı. Kısa süre sonra televizyonda Magnus’un yüzü belirdi. İlk hamleyi yapmak üzereydi. Elini C2 deki piyona götürdü ve iki kare ileriye doğru ilk hamlesini yaptı. Televizyonda şimdi Fabian’ın yüzü vardı…
Sizce müsabakayı Magnus kazanırsa Dünya sıralamasındaki güncel puanı ne olur? Peki ya Magnus kazanırsa, Fabiano ne kadar geriye düşer? Ya tam tersi durumda?
Satranç federasyonunun bu 4 haneli puan hesabı için bir katsayı belirlediğini düşünelim. Bu sayı 24 olsun. Buna göre müsabakayı Magnus kazanırsa aşağıdaki gibi bir durum oluşur.
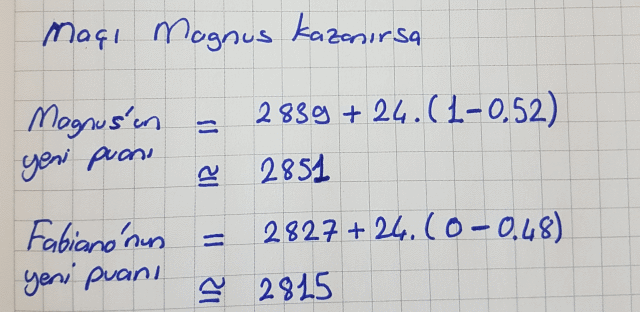
İki satranç ustası arasındaki fark biraz daha açılıyor görüldüğü gibi. Aksine maçı Fabiano kazanırsa, birinci ve ikinci sıradakiler yer değiştirecek gibi görünüyor. Aşağıdaki gibi hesaplamayı devam ettirebiliriz.

Formülasyondaki 24 değeri satranç federasyonu tarafından belirlenmiş bir katsayı. İyi bir hesaplama için bu katsayının 10 ile 32 aralığında olması öneriliyor. Maçı kazanma durumunda 1, kaybetme durumunda da 0 sayıları kullanılmakta(Beraberlik şu an için hesaba kattığımız bir kriter değil) Ayrıca yarışmacıların güncel puanları ve buna göre hesaplanmış kazanma olasılıkları da eşitliğin içerisinde yer alıyor.
İtiraf ediyorum işlemleri kolayca yapabilmek için hesap makinesi yerine node.js komut satırından yararlandım :)
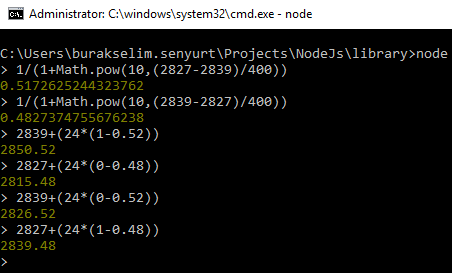
Magnus ve Fabiano ilk iki sırada yer alan oyuncular ve ELO rating değerleri birbirlerine oldukça yakın. Lakin puan farkının daha fazla olduğu bir durum söz konusu olursa maç sonucundan oyuncuların çok daha farklı etkileneceklerini söyleyebiliriz. Kazanma oranı çok yüksek olan bir oyuncunun puanında önemli bir artış olmayacak ama kazanma ihtimali düşük olan oyuncunun galip gelmesi halinde kendi puanındaki artış yüksek olacaktır.
Bu durumu irdelemek için Magnus ile 100ncü sırada yer alan Çek satranç ustası Igors Rausis arasında bir maç yapıldığını düşünelim. Magnus’un maçı kazanma olasılığı güncel puanına göre %75, Igors’un kazanma olasılığı ise %25 olarak hesaplanır. Eğer maçı Magnus kazanırsa puanı 2845 olur. 6 puanlık bir artış. Bu noktada maçı kaybeden Igors’un puanıda 6 puanlık düşüşle 2645'e iner.
Peki ya maçı Igors kazanırsa? Bu durumda Igors’un puanı 18 puan artarak 2669 olur. Magnus’da aynı değerde puan kaybedecektir(2821) Aslında birbirlerinden aynı değerde puan kazandıklarını/kaybettiklerini söyleyebiliriz. Tabii noktadan sonraki hassaslığı arttırır ve katsayıyı değiştirirsek puanlardaki artış ve azalma aralıklarını da etkileyebiliriz.
Kullanılan eşitlikleri formülüze etmek istersek aşağıdaki denklemler ortaya çıkacaktır.

Aslında ELO rating değerini hesaplarken yararlanılabileceğimiz bir eğri de bulunmaktadır. Kazanma olasılığı ve oyuncular arasındaki ELO puan farkını hesaba katan bu eğri aşağıdaki gibidir.
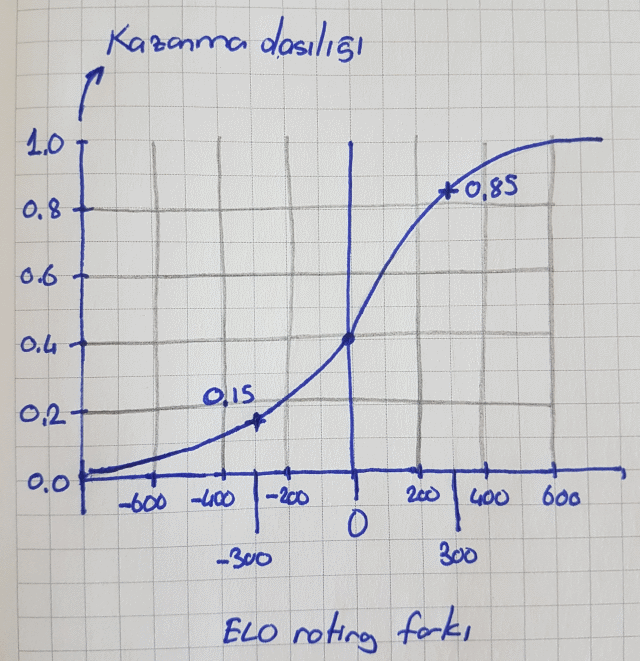
Söz gelimi iki yarışmacının güncel ELO puanları arasındaki fark 300 olsun. Pozitif taraftan bakarsak puanı yüksek olan yarışmacının %85 kazanma olasılığına sahip olduğunu söyleyebiliriz. Buna göre rakibinin kazanma olasılığı da eksi değerin olduğu eğrideki kesişim noktasıdır. Yani %15.
ELO oranı bugün League of Legends gibi çok oyunculu platformlarda dahil olmak üzere bir çok oyunda kullanılıyor. Eğer hoşunuza gittiyse tenis oyuncularının rating değerlerini ele alıp aralarında maçlar yaptırarak güncel puanlamalarını öğrenebilirsiniz. Hatta bu formülasyonu koda dökerek, geliştireceğiniz farklı ürünlerde değerlendirebilirsiniz(Zuckerberg’in Harvard’da Facemash için ELO rating algoritmasını kullandığı söylentisi bile var örneğin. Bu tartışma için Quora'ya bakılabilir)
Profesör Arpad Elo’nun 95 yıllık yaşamında insanlığa kattığı önemli değerlerden birisi olan bu hesaplama tekniği, yarışmacıları övmek veya yargılamak yerine adil bir puantaj sistemi ile sıralanmasında büyük rol oynamakta. Üstelik bu formül sistemi 1950den beri hayatımızda…