Merhaba Arkadaşlar,

[İlk Draft Tarihi : 2012-08-01]

Bundan bir kaç sene önce ünlü matematikçi Fermat’ nın son teoreminin nasıl ispat edildiğinin anlatıldığı bir kitabı okumuştum. 1670 yılında ortaya çıkan ve Fermat tarafından o zaman ispat edildiği öne sürülen ama bildiğim kadarı ile kanıt bulunamayan teorem ancak 1995 yılında Andrew Wiles tarafından kanıtlanabilmiştir.  

Söz konusu teoremin ispatı sırasında(bununla ilişkili olarak wikiden bilgi alabilirsiniz) arada ispat edilmek zorunda kalınan başka teoremler de ortaya çıkmıştı. Kitabın içerisinde altın orandan tutunda, Şimuya-Taniyama konjöktörünün çözümlenmesine kadar pek çok konuya yer verilmişti. Şimdi haklı olarak bunları niye söylüyorsun diyeceksiniz?

Görünen o ki evrenin hemen her alanında matematiğin izlerine rastlamaktayız. İşin gerçeği bildiğimiz tüm bilimler illaki bir ucundan da olsa matematiğe bulaşmak zorunda kalmıştır/kalmaktadır/kalacaktır. Söz gelimi bilgisayar bilimlerini göz önüne alalım. Bilgisayar bilimleri deyince işin içerisine elektronikten tutunda yazılıma kadar geniş bir alan girmektedir. Hatta kapalı ve açık devre ile başlayan ampüllerin zaman içerisinde 1 ve 0’ lar olarak anıldığı ve karşımıza anlamlı, işlenebilir veri olarak çıktığı bir durum da söz konusudur.

1 ve 0’ lar dediğimiz de ise çok basit olarak matematikteki sayı sistemlerine değinmemiz kaçınılmazdır. İkili(Binary) sayı sistemi aslına bakıldığında makinanın anlayabileceği tek kavram olarak görünmektedir. Sonuç itibariyle devrelerin çalıştığı sinyaller göz önüne alındığında open ve close durumlarının oluşması gerekir. Makinenin dip noktasından daha yukarılara doğru çıktığımızda ise karşımıza ondalık(decimal), sekizli(octal) ve hatta 16lık(Hexadecimal) sayı sistemleri çıkmaktadır. Bu sayı sistemleri arasında belirgin farklılıklar vardır elbette. Her şey byte seviyesinde düşünüldüğünde 8bitlik 1ler ve 0lar dizisine dönüşüyor olsa da, verilerin saklanması gerektiği durumlarda diğer sayı sistemleri ve özellikle hexadecimal yapı oldukça ön plana çıkabilmektedir.

İlk olarak biraz matematik diyeceğiz ve binary, decimal ile hexadecimal sayı sistemlerini göz önüne alıyor olacağız. Aşağıdaki şekilde çok basit olarak bu sayı sistemlerindeki temel değerlerin karşılıkları gösterilmektedir.

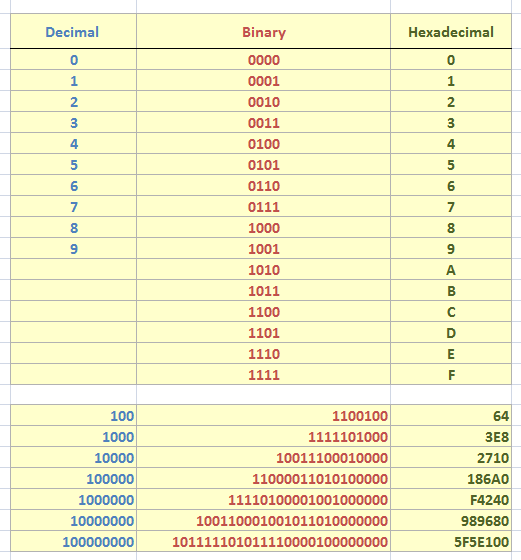
Bilindiği üzere decimal sayılar 0dan 9a kadardır. Binary sayıların sadece 1 ve 0 olduğunu biliyoruz. Diğer yandan Hexadecimal sayılar 0dan 9a kadar decimal sayılar şeklinde iken sonrasında A,B,C,D,E ve F olarak devam etmektedirler. Özellikle bir ondalıklı sayının ikili düzendeki ifadesine baktığımızda  hane sayısı oldukça fazla olan rakam dizileri ile karşılaşmamız normaldir. Ancak hexadecimal düzene baktığımızda ise ondalıklı sayılara göre daha az haneden oluşan diziler söz konusu olmaktadır. Söz gelimi 100000000, 9 hanelidir ve binary karşılığı 27 rakamdan oluşmaktadır. Oysaki bu sayının hexadecimal karşılığı 7 hanedir. Hiç yoktan 2 hane 2 hanedir. Bir kum tanesi olarak düşünüldüğünde bir anlam ifade etmeyebilir ama bir kamyon dolusu kum düşünüldüğün daha büyük bir kazançta sağlayabilir

Tabi burada hane sayısının azalmasının veya fazla olmasının, makine seviyesinde bakıldığında bir anlam ifade etmediğini vurgulamamız gerekiyor. Nitekim makine seviyesinde herşey mutlak suretle 1 ve 0 olarak ifade edilmek durumundadır.

Peki matematiksel olarak bu sayı sistemleri arasındaki dönüşümler nasıl yapılabilir? Özellikle ondalıklı sistemdeki sayıların ikili düzende ifade edilmesi veya hexadecimal’ e çevrilmesi nasıl gerçekleştirilmektedir?

Burada olayı biraz kağıt kalem kullanarak ve basit bölme ve üst alma işlemleri yaparak ele almamız gerekmektedir. Örneğin 78 sayısının ikili düzendeki karşılığını bulalım ve ters dönüşümünü de sağlayalım. İşte örnek çalışma;

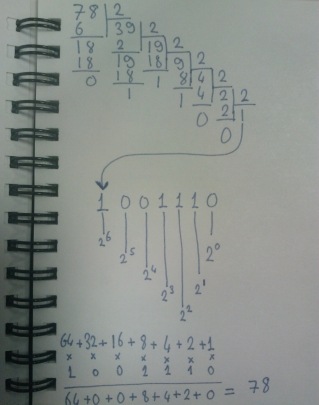
Yazımın kötü olmasından dolayı gerçekten çok üzgünüm. Dikkat edileceği üzere ikili sisteme dönüştürme işlemi için sayının sürekli olarak 2’ye bölünmesi ve kalan 1 ve 0 ların ters sırada birleştirilmesi söz konusudur. İkili sayı sisteminde ifade edilen rakamların, ondalık sisteme dönüştürülmesinde ise, 2üzeri0 dan başlayaraktan 2nin katları ile 1 ve 0ların çarpımı sonucu elde edilen ifadelerin toplanması söz konusudur.

Peki 78 sayısının hexadecimal karşılığı nasıl bulunabilir? ve tabi hexadecimal bir sayının ondalık sistemdeki karşılığı nasıl hesaplanır? Yine kağıt kaleme sarılırsak işlemin çok daha basit olduğunu görebiliriz.

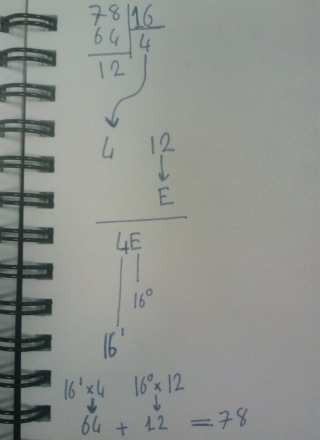
Görüldüğü üzere bir ondalıklı sayının ikili sisteme dönüştürülmesindeki felsefenin aynısı burada da geçerlidir. Tek yapılması gereken 16ya bölme ve kalanları değerlendirmedir. Tabi kalanarın 1 ve 0 değil, 0 ile 15 aralığında olması önemlidir. 9dan sonraki rakamlarda(10,11,12,13,14,15) sırasıyla A,B,C,D,E ve F harflerine yer verilmektedir. Bir hexadecimal ifadenin ondalıklı sayıya çevrilmesinde ise 16üzeri0 ile başlayan katlı sistem devreye girer. İlgili katlar sayının veya harfin karşılık geldiği(örneğin Enin karşılığı olan 12) değer ile çarpılır ve genel toplam alınarak ondalık sayı karşılığı bulunur.

Teorem bu kadar basit olduğuna göre bir sayının ikili veya 16lı sayı sistemine çevrilmesi için gerekli kodları geliştirebilirsiniz. Bu iyi bir antrenman olacaktır Ama çok da şart değildir. Nitekim Convert tipinin ilgili static metodları base parametresi ile ilgili dönüşümlere izin vermektedir. Aşağıdaki örnek kod parçasını bu anlamda göz önüne alabiliriz.

using System;

namespace NumberSystems 
{ 
    class Program 
    { 
        static void Main(string[] args) 
        { 
            int number1 = 78; 
            string number1Binary = Convert.ToString(number1, 2); 
            string number1Hexadecimal = Convert.ToString(number1, 16);

            Console.WriteLine("Decimal to Binary/Hexadecimal\n{0}\t=\t{1}\n{2}\t=\t{3}\n" 
                ,number1 
                ,number1Binary 
                ,number1 
                ,number1Hexadecimal 
                );

            int number2 = Convert.ToInt32(number1Binary, 2); 
            int number3 = Convert.ToInt32(number1Hexadecimal, 16);

            Console.WriteLine("Binary/Hexadecimal to Decimal\n{0}\t=\t{1}\n{2}\t=\t{3}\n" 
                , number1Binary 
                , number2 
                , number1Hexadecimal 
                , number3 
                ); 
        } 
    } 
}

Convert tipinin static ToString ve ToInt32 metodlarına verilen ikinci parametrelere dikkat edelim. Bu parametreler ile sayısal taban belirtilmektedir. Binary düzen için 2, Hexadecimal düzen için ise 16. Kodun çalışma zamanı çıktısı ise aşağıdaki gibi olacaktır.

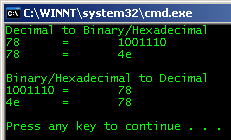
Şimdi olayı biraz daha ilginç bir hale getirelim ne dersiniz? Önce örnek kodumuz…

using System; 
using System.Collections.Generic; 
using System.IO; 
using System.Text;

namespace NumberSystems 
{ 
    class Program 
    { 
        static void Main(string[] args) 
        { 
            string fileDecimal = Path.Combine(Environment.CurrentDirectory, "Decimal.txt"); 
            string fileBinary = Path.Combine(Environment.CurrentDirectory, "Binary.txt"); 
            string fileHexadecimal = Path.Combine(Environment.CurrentDirectory, "Hexadecimal.txt");

            List<int> numbers = GetRandomNumbers(100000000, 900000000, 1000000);

            WriteToFile(fileDecimal, numbers, BaseType.Decimal); 
            WriteToFile(fileBinary, numbers, BaseType.Binary); 
            WriteToFile(fileHexadecimal, numbers, BaseType.Hexadecimal); 
        }

        private static List<int> GetRandomNumbers(int initialValue, int lastValue, int arrayLength) 
        { 
            List<int> numbers = new List<int>();

            Random random = new Random(); 
            for (int i = 0; i < arrayLength; i++) 
            { 
                numbers.Add(random.Next(initialValue, lastValue)); 
            }

            return numbers; 
        } 
        private static void WriteToFile(string fileName, List<int> numbers, BaseType baseType) 
        { 
            StringBuilder builder = new StringBuilder();

            for (int i = 0; i < numbers.Count; i++) 
            { 
                builder.AppendLine(Convert.ToString(numbers[i], (int)baseType)); 
            }

            File.WriteAllText(fileName, builder.ToString()); 
        } 
    }

    public enum BaseType 
    { 
        Binary = 2, 
        Decimal = 10, 
        Hexadecimal = 16 
    } 
}

Öncelikle bu kod parçasında ne yaptığımıza bir bakalım.

GetRandomNumbers isimli metodumuz belirtilen integer değer aralığında bizim belirttiğimiz sayıda rastege sayı üretmekte ve bunları generic bir List<int> koleksiyonu içerisinde geriye döndürmektedir. WriteToFile isimli metodumuz ise bu rastgele sayı listesini alıp fiziki bir text dosyasına kayıt etmektedir. WriteToFile metodunun üçüncü parametresi BaseType enum sabiti tipindendir. Bu sabite dikkat edecek olursak Binary, Decimal ve Hexadecimal sayı tabanı sistemlerini işaret edecek şekilde oluşturulmuştur. İlgili Enum sabitinin sayısal değeri, Convert.ToString metodunun ikinci parametresi olarak kullanılmaktadır. Main metodu içerisinde yazdığımız test kodları, ondalıklı sayıların decimal, binary ve hexadecimal düzende tutulduğu text dosyalarının üretimini üstlenmektedir. Kodun yazılış biçiminden ziyade, kullanılan senaryo gereği üretilen dosya boyutlarının ne olduğu daha çok önemlidir. İşte bu denemenin sonuçları.

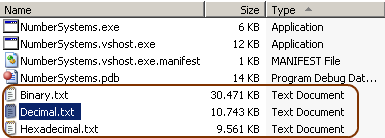
Mutlaka dikkatinizi çekmiştir ki, Binary dosya boyutu 30 megabyte ile haklı bir liderliği üstlenmektedir Her ne kadar Decimal ile Hexadecimal arasında çok büyük bir fark olmadığı gözüksede, sayı dizisinin boyutunun arttırılması halinde durum biraz daha farklılık gösterebilmektedir. Bu amaçla test sonuçlarını biraz daha sağlıklı irdelemek adına kodumuzu biraz daha değiştirelim.

using System; 
using System.Collections.Generic; 
using System.Diagnostics; 
using System.IO; 
using System.Text;

namespace NumberSystems 
{ 
    class Program 
    { 
        static void Main(string[] args) 
        { 
            string fileDecimal = Path.Combine(Environment.CurrentDirectory, "Decimal.txt"); 
            string fileBinary = Path.Combine(Environment.CurrentDirectory, "Binary.txt"); 
            string fileHexadecimal = Path.Combine(Environment.CurrentDirectory, "Hexadecimal.txt");

            for (int i = 5; i < 9; i++) 
            { 
                int length = (int)Math.Pow(10, i); 
                Console.WriteLine(length); 
                List<int> numbers = GetRandomNumbers(10000000, 90000000, length); 
                WriteToFile(fileDecimal, numbers, BaseType.Decimal); 
                WriteToFile(fileBinary, numbers, BaseType.Binary); 
                WriteToFile(fileHexadecimal, numbers, BaseType.Hexadecimal); 
                Console.WriteLine("---"); 
            } 
        }

        private static List<int> GetRandomNumbers(int initialValue, int lastValue, int arrayLength) 
        { 
            List<int> numbers = new List<int>();

            Random random = new Random(); 
            for (int i = 0; i < arrayLength; i++) 
            { 
                numbers.Add(random.Next(initialValue, lastValue)); 
            }

            return numbers; 
        } 
        private static void WriteToFile(string fileName, List<int> numbers, BaseType baseType) 
        { 
            StringBuilder builder = new StringBuilder(); 
            Stopwatch watcher = new Stopwatch();

            for (int i = 0; i < numbers.Count; i++) 
            { 
                builder.AppendLine(Convert.ToString(numbers[i], (int)baseType)); 
            }

            watcher.Start(); 
            File.WriteAllText(fileName, builder.ToString()); 
            watcher.Stop(); 
            FileInfo fi=new FileInfo(fileName); 
            Console.WriteLine( 
                "{0}\tSize:{1}\tProcess Time:{2}" 
                ,Path.GetFileName(fileName) 
                ,fi.Length.ToString() 
                ,watcher.ElapsedMilliseconds.ToString() 
                ); 
        } 
    }

    public enum BaseType 
    { 
        Binary = 2, 
        Decimal = 10, 
        Hexadecimal = 16 
    } 
}

Bu sefer 10un katları şeklinde arka arkaya denemeler yapıyoruz. Her denemede binary, decimal ve hexadecimal dosyalardan birer tane üretmekteyiz. Sonuçları daha sağlıklı irdelemek adınaysa ekrana üretilen dosyanın adını, boyutunu, test için kullanılan eleman sayısını ve son olarakta yazma işlemi sırasında geçen süreleri çıkartmaktayız. Her test sırasında farklı sayılar ile çalışılıyor olasa teste tabi tutulan eleman sayısı belirleyici kriter olduğundan bu durumu göz ardı edebiliriz. Uygulamanın çalışma zamanındaki çıktısı aşağıdaki gibi olacaktır.

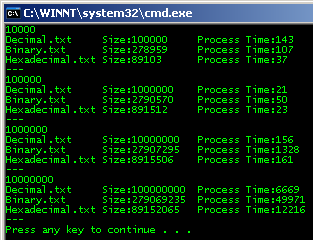
Tabi söz konusu istatistikleri Excel üzerine grafik haline getirdiğimizde durumu biraz daha net bir biçimde analiz edebiliriz. İlk olarak üretilen dosya boyutlarına bir bakalım.

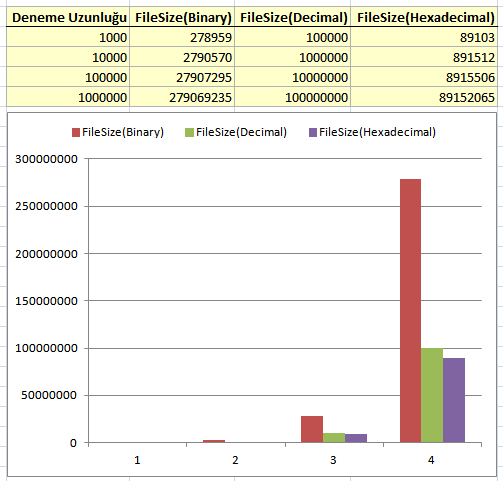
İlk başlarda çok fazla fark görülmüyor olsa da, eleman sayısının çok daha fazlalaştırılması halinde özellikle binary düzende saklanan veri kümesinin toplam boyutunun belirgin ölçüde yükseldiği gözlenmekte. Dosyalara yazma sürelerine ait istatistikler de aşağıdaki gibi özetlenebilir.

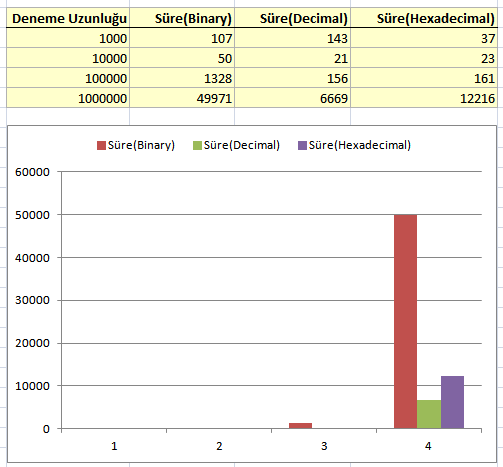
Aslında en hızlı üretim biçimi decimal içerikli dosyalarda söz konusudur. Ancak hız ve boyut kriterlerine baktığımızda Hexadecimal olarak veriyi saklamanın daha uygun olduğu sonucuna varılabilir. Tabi şu durum da gözden kaçırılmamlıdır. Decimal içerikleri Hexadecimal olarak saklamak ve bu saklanan içeriği tekrardan decimal olarak göstermek istediğimizde yazma ve okuma işlemleri yapılması gerektiği ve bunlar için uygulamaya ek süreler yükleneceği de ortadadır. Yine de bazı bilimsel ve matematiksel uygulamalarda, çok büyük boyutlu decimal içeriklerin fiziki olarak saklanması gerektiği durumda Hexadecimal çevirmeler düşünülebilir. Böylece geldik bir yazımızın daha sonuna. Tekrardan görüşünceye dek hepinize mutlu günler dilerim.

NumberSystems.zip (25,96 kb)